Gli esami di maturità 2023 sono attualmente in corso e, alla seconda prova del Liceo Scientifico, la prova di matematica ha gettato nel panico moltissimi studenti per i quiz riguardanti il Teorema di Rolle. Ma in cosa consiste questo Teorema? E come vanno risolti questi quesiti? Andiamo a scoprirlo insieme.
- Che cosa dice il Teorema di Rolle?
- Il Teorema di Rolle sulla maturità 2023: il quesito proposto ai maturandi
Che cosa dice il Teorema di Rolle?
Andiamo con ordine e partiamo dal principio. Il teorema di Rolle è un importante risultato del calcolo differenziale che stabilisce una condizione necessaria per l’esistenza di almeno un punto nel dominio di una funzione in cui la sua derivata si annulla.
Scopri anche:– Il test matematico che solo 1 su 1000 riesce a risolvere
La formulazione del teorema di Rolle è la seguente: supponiamo di avere una funzione continua f(x) definita nell’intervallo chiuso [a,b] e derivabile in ogni punto dell’intervallo aperto (a,b). Se f(a) = f(b), cioè se i valori della funzione agli estremi dell’intervallo sono uguali, allora esiste almeno un punto c in (a,b) tale che la derivata prima di f nel punto c sia zero, ovvero f′(c) = 0.
Detta in termini più semplici, possiamo dire che il teorema di Rolle afferma che se una funzione è continua su un intervallo chiuso e derivabile in ogni punto all’interno di quell’intervallo, e se i valori della funzione agli estremi dell’intervallo sono uguali, allora c’è almeno un punto all’interno dell’intervallo in cui la derivata si annulla.
Un modo intuitivo per comprendere il teorema è quello di provare ad immaginare una funzione che rappresenta il percorso di un oggetto in movimento. Se l’oggetto parte da un punto e arriva allo stesso livello dopo un certo intervallo di tempo, allora in qualche momento durante il tragitto l’oggetto deve aver avuto velocità zero, cioè si è fermato. Il teorema di Rolle formalizza questa idea per le funzioni matematiche.
Il Teorema di Rolle sulla maturità 2023: il quesito proposto ai maturandi
Il quesito sul Teorema di Rolle della maturità 2023 è una prova piuttosto complicata, che recita così:
Si consideri la funzione:
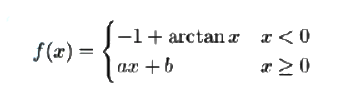
funzione teorema di rolle
- Determinare per quali valori dei parametri reali a, b la funzione è derivabile.
- Stabilire se esiste un intervallo di R in cui la funzione f soddisfa le ipotesi del teorema di Rolle. Motivare la risposta.
Nella prima parte dell’esercizio occorre studiare la continuità della funzione, calcolandone il limite sinistro e poi il limite destro. Quindi, bisogna studiare la derivabilità della funzione.
Al termine del calcolo, si otterrà che a = 1.
È a questo punto che interviene il teorema di Rolle, che abbiamo illustrato sopra.
Poiché abbiamo identificato i valori dei parametri per cui la funzione è continua e derivabile su tutto R, per tali valori lo sarà sicuramente in ogni intervallo chiuso [a,b], verificando le prime due ipotesi del teorema. Pertanto, dobbiamo chiederci se esistono due valori a e b in cui f(a) = f(b).
Si può quindi osservare che la funzione è sempre strettamente crescente (positiva). Per tale ragione, la funzione non può assumere valori uguali in due punti distinti, e pertanto il teorema di Rolle non può essere applicato.











